MEAM 211 is an undergraduate-level dynamics course taken by all mechanical engineering sophomores, covering fundamental techniques for modeling the dynamics of mechanical systems. While much of the course is focused on symbolic analysis, a computational component has become more of a focus in recent years.

As a Head TA for one semester, my role in the teaching team included developing computational assignments in MATLAB, designing and leading interactive problem solving recitations, and working directly with students in office hours on challenging homework problems and essential course concepts. I appreciated the guidance of Prof. Michael Posa and the collaboration of my co-Head TA Jessica Weakly, along with the masters student TA’s.

Course Overview

MEAM 211 is a core requirement for undergraduate mechanical engineers, with several expected learning outcomes that are essential in mechanical engineering practice and analysis:

1. First-Principles Modeling of Mechanical Systems

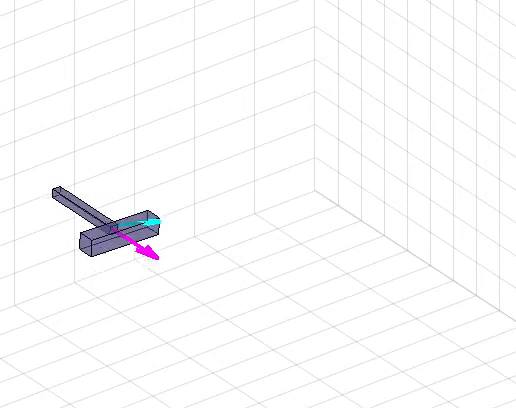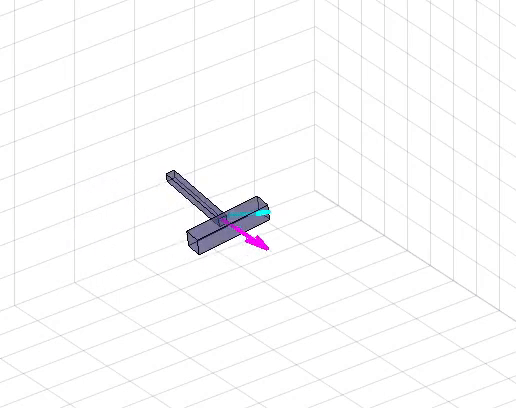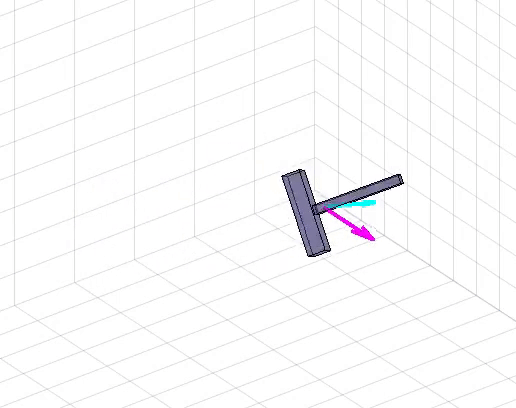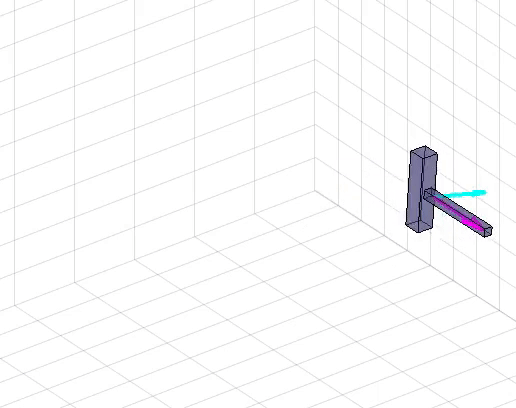
By studying the Newton-Euler dynamics of a rigid body in 3D, and learning to compose those models via interconnecting elements like joints and springs, students learn a rigorous framework to derive the equations of motion of arbitrary mechanical systems.

2. Building General Computational Tools for Dynamics

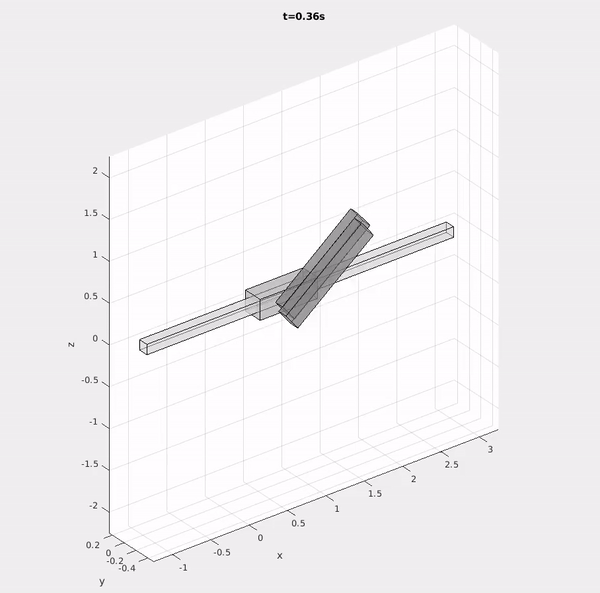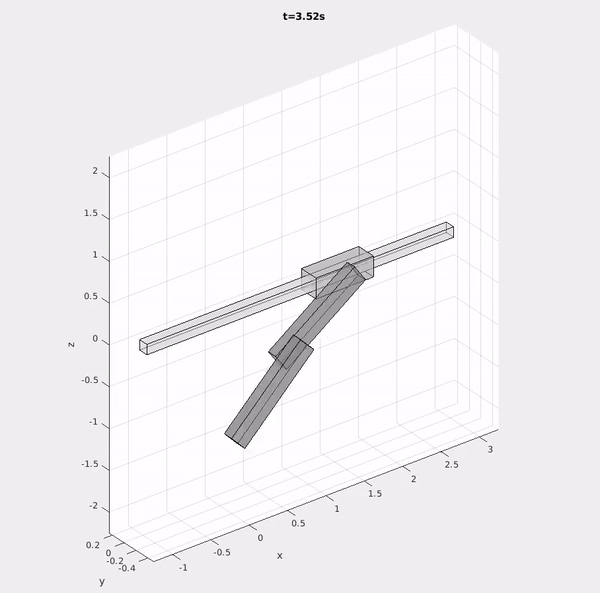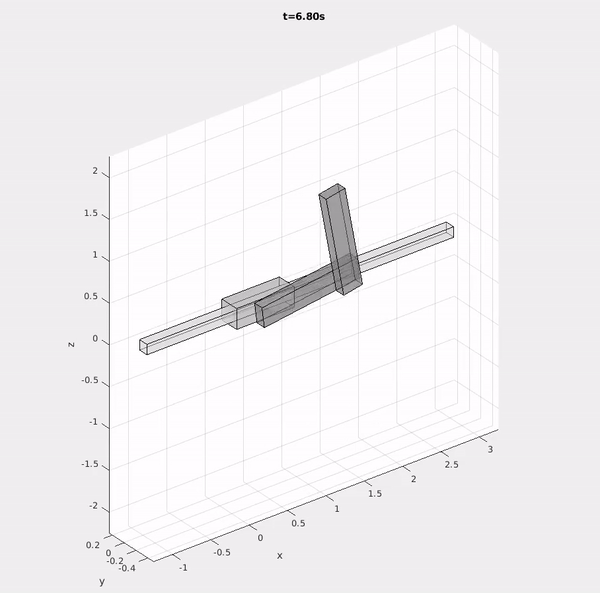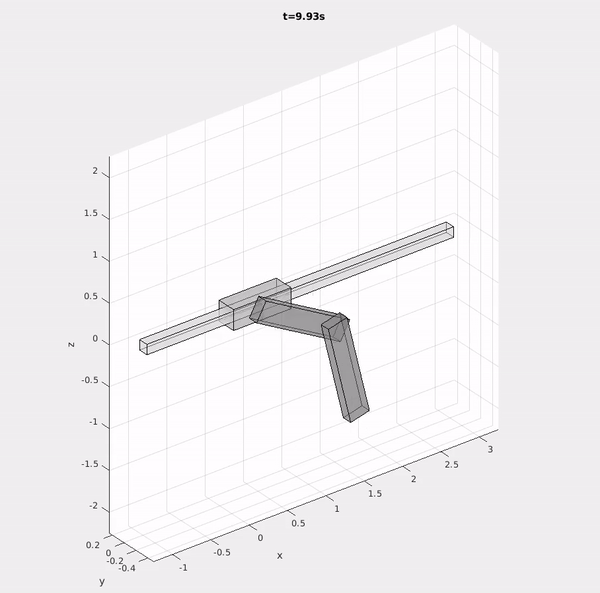
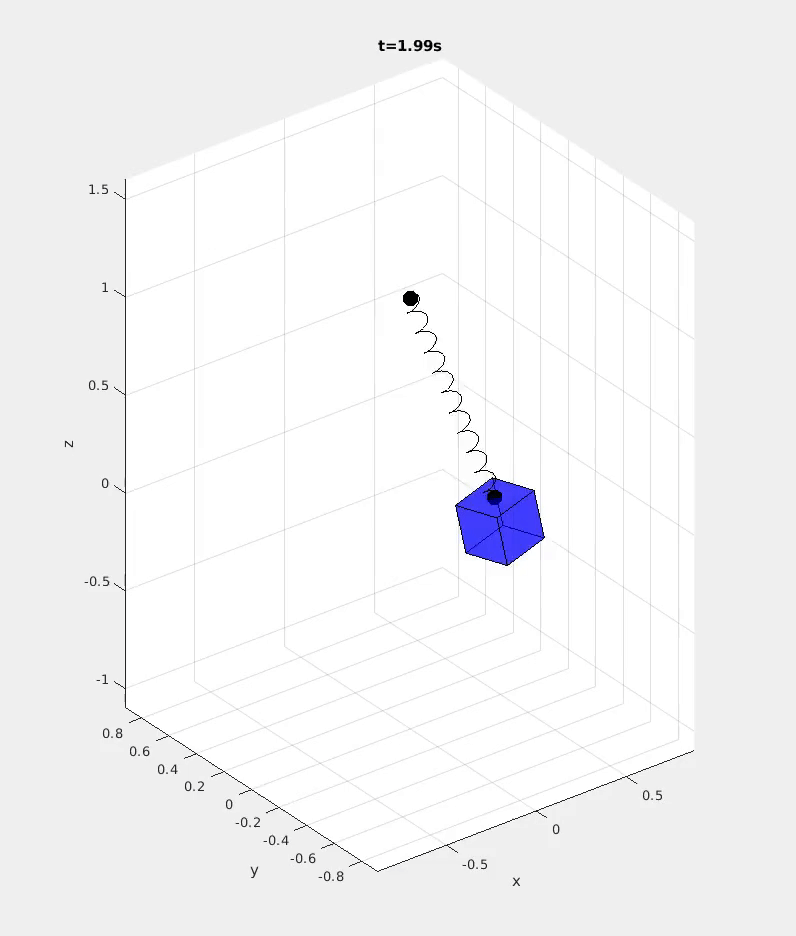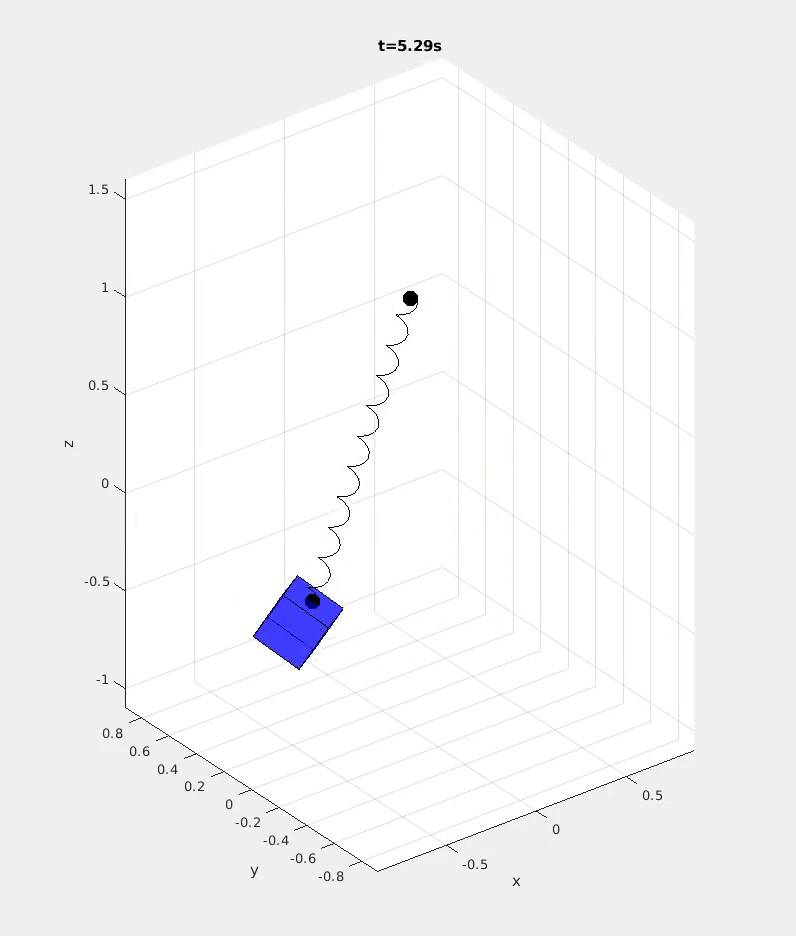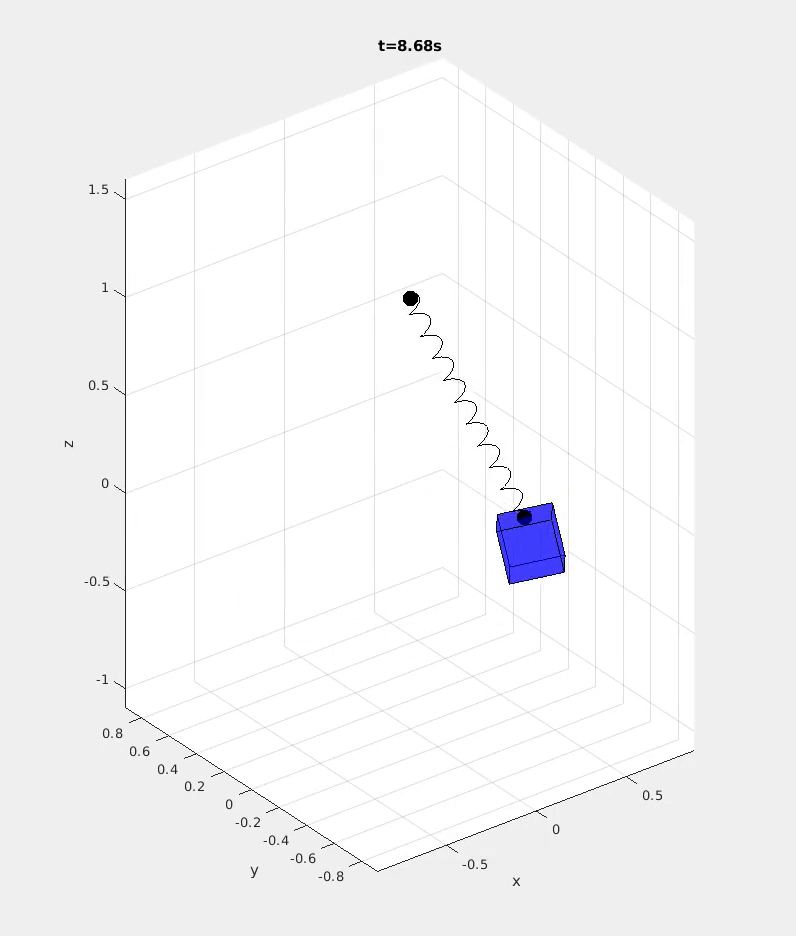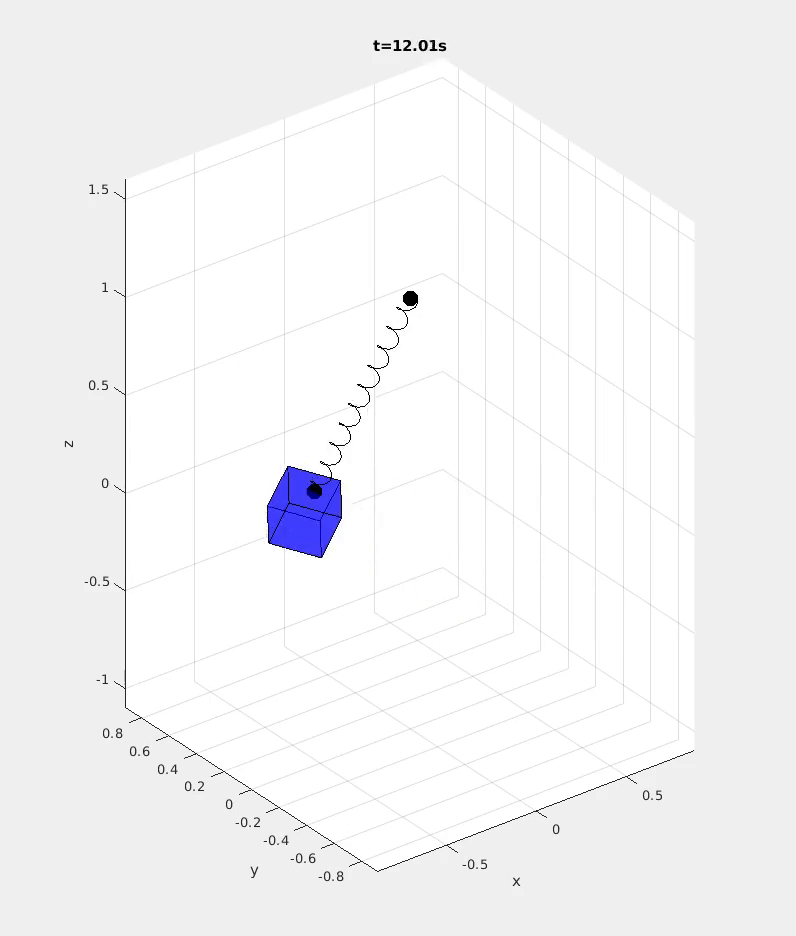
Because the equations of motion of coupled systems of rigid bodies quickly become intractible to derive or manipulate by hand, students learn to implement the underlying mathematical models in software. Via weekly step-by-step assignments, students gradually complete the features necessary to model and simulate arbitrary rigid body systems by exploiting a kinematic tree structure and recursion.

3. Using Conserved Quantities for System Analysis

Mechanical systems enjoy symmetries that lead to conserved quantities as described by Noether’s Theorem. These conservation laws can simplify analysis, and can also be used as a “sanity check” to quickly point out implementation errors in a numerical simulation.

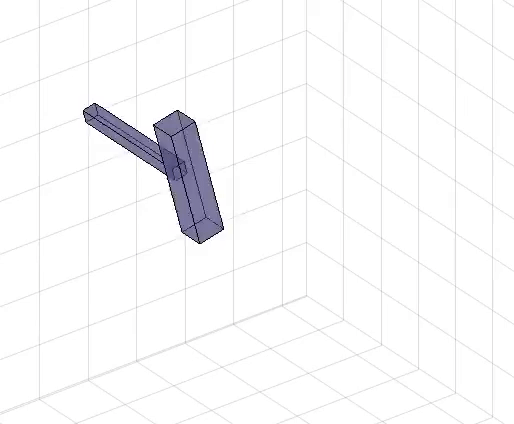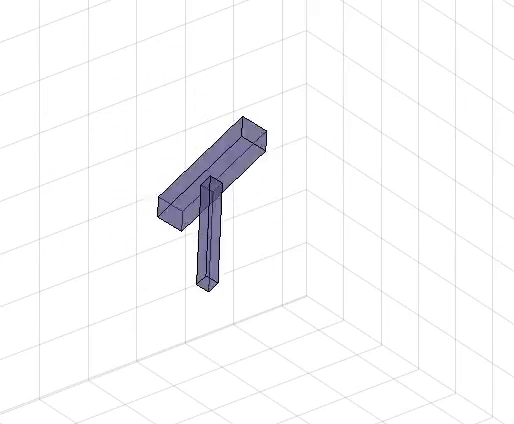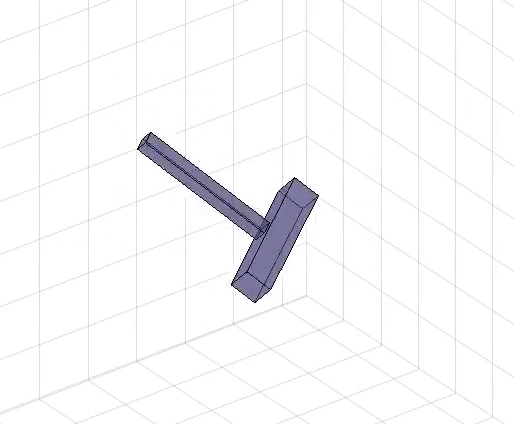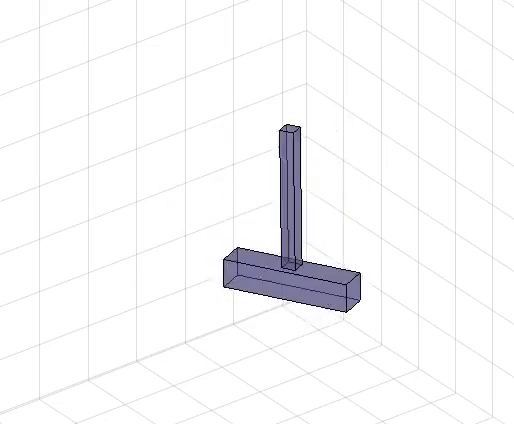
My Teaching Role

Alternating weeks with my co-Head TA, I was responsible for designing and leading interactive problem-solving recitations to complement the lecture material, comprising a mixture of individual and group work on analysis and computation problems and sometimes supplemented by coding exercises in MATLAB. I also enjoyed working closely with students in office hours to clear any remaining doubts.

In addition to working directly with students, I took on a significant role in the development of the computational assignments led by Prof. Michael Posa. I designed a portion of the simulator architecture, developed the testing infrastructure students could use to verify their solutions, and designed engaging demonstrations of the simulator to motivate students in their work.